“ quantum computing can solve problems that classical computers can’t ”
Have you ever heard the above statement? In this article, we will explore the potential of quantum computing to solve complex problems and examine the concept of Bounded-Error Quantum Polynomial-Time (BQP) and its relationship to the classical complexity class. We will consider the basics of quantum computing, providing intuition for what BQP is and how it differs from classical computing models.

Classical Complexity Classes
The world of theoretical computer science is full of fascinating concepts and one of the most interesting of them all is the Complexity Class. This is the study of
how long it takes for a classical computer to solve different types of problems?
Two of the most important complexity classes are P and NP.
P stands for “polynomial time” and it represents the set of all problems that can be solved in a reasonable amount of time by a classical computer.
NP stands for “nondeterministic polynomial time” and it represents the set of all problems that have a solution that can be verified in a reasonable amount of time by a classical computer.
If you ever thought to yourself, what is the hardest way of winning $1M? It is probably decades whether all problems in NP can also be solved in polynomial time or
If the solution to a problem is easy to check for correctness, must the problem be easy to solve?
Clearly, P ⊆ NP, but the above asks if P = NP. This is known as the P *vs** **NP* problem and it is considered one of the most important open problems in theoretical computer science. A solution to this problem would give The solver a $1M prize since P *vs** **NP **is mentioned as one of the Millennium Prize Problems (it is widely believed that **P* ≠ NP)
PSPACE stands for “polynomial space” and it represents the class of problems that can be solved using a polynomial amount of space on a classical computer. It is a complexity class that contains both P and NP, and it is considered a larger class than both of them. In other words, any problem that can be solved in polynomial time or polynomial space is also a PSPACE problem.
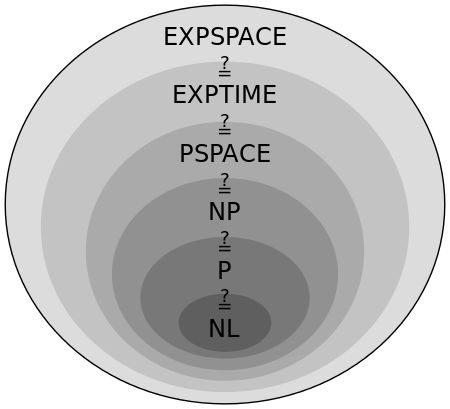
Another interesting concept is the Time Hierarchy Theorem, which states that for any complexity class, there exists a problem that can be solved in a time that grows faster than a polynomial function. In simpler terms, it means that there is no upper limit to how complex a problem can be, and it is not known where the hierarchy collapses in the above diagram.
**Quantum **Complexity Classes
bounded-error quantum polynomial time (BQP) **is a complexity class that describes the class of problems that can be solved on a quantum computer in polynomial time with a bounded probability of error. This class of problems is considered to be the “sweet spot” for quantum computing, as it represents a balance between the power and limitations of quantum computing, in particular with an error probability of at most 1/3 for all instances
One of the most important and well-known problems in **BQP **is Shor’s algorithm, which is a quantum algorithm for factoring integers. It is exponentially faster than the best-known classical algorithm for this task and has the potential to break many of the modern cryptographic systems that rely on the difficulty of factoring large integers.
Another important problem in *BQP **is the *Quantum Approximate Optimization Algorithm (QAOA), which is a quantum algorithm for solving optimization problems. It has been shown to be more efficient than classical algorithms for certain types of optimization problems and has potential applications in fields such as machine learning and logistics.
P ⊆ BQP
Now let’s go back to the Complexity Hierarchy [1] shows that every classical circuit can be simulated by a quantum circuit, thus given a classical instant of a P problem we can generate an equivalent quantum circuit i.e. P ⊆ BQP.
In terms of Time Complexity, *let’s give an upper bound for BQP.* We begin with an easier containment BQP ⊆ EXP-SPACE, and then we will give a tighter bound BQP ⊆ P-SPACE, since P-SPACE ⊆ EXP-SPACE. I will just give an intuition for that, and not a formal proof, but for those who do not feel comfortable with these ideas, I suggest skipping the 2nd part.
1. BQP ⊆ EXP-SPACE
APPROX-QCIRCUIT-PROB(AQP) is a problem related to quantum computing that involves estimating the probability of certain outcomes when measuring a quantum circuit. Any problem in BQP **is as **hard **as APPROX-QCIRCUIT-PROB, meaning that if we can solve APPROX-QCIRCUIT-PROB, we can solve any other problem in **BQP. The idea behind the proof of BQP ⊆ EXP-SPACE is simple. Since we have exponential power, given a quantum circuit C, we can use a classical computer to stimulate each gate in C to get the final state.
2. BQP ⊆ P-SPACE
We will prove that BQP⊆ **P-SPACE. **To do so, we will need to use a technique called the Sum of Histories[2]. This technique is a way to visualize the evolution of a quantum state in a quantum circuit. It is used to solve the APPROX-QCIRCUIT-PROB problem.
The technique involves visualizing the circuit as a tree, with the input as the root and each gate as a level of the tree. The transition amplitude of a root-to-leaf path is the product of all the weights on the edges along the path. To calculate the probability of the final state, we sum up the amplitudes of all root-to-leaf paths that end at a node representing that final state.
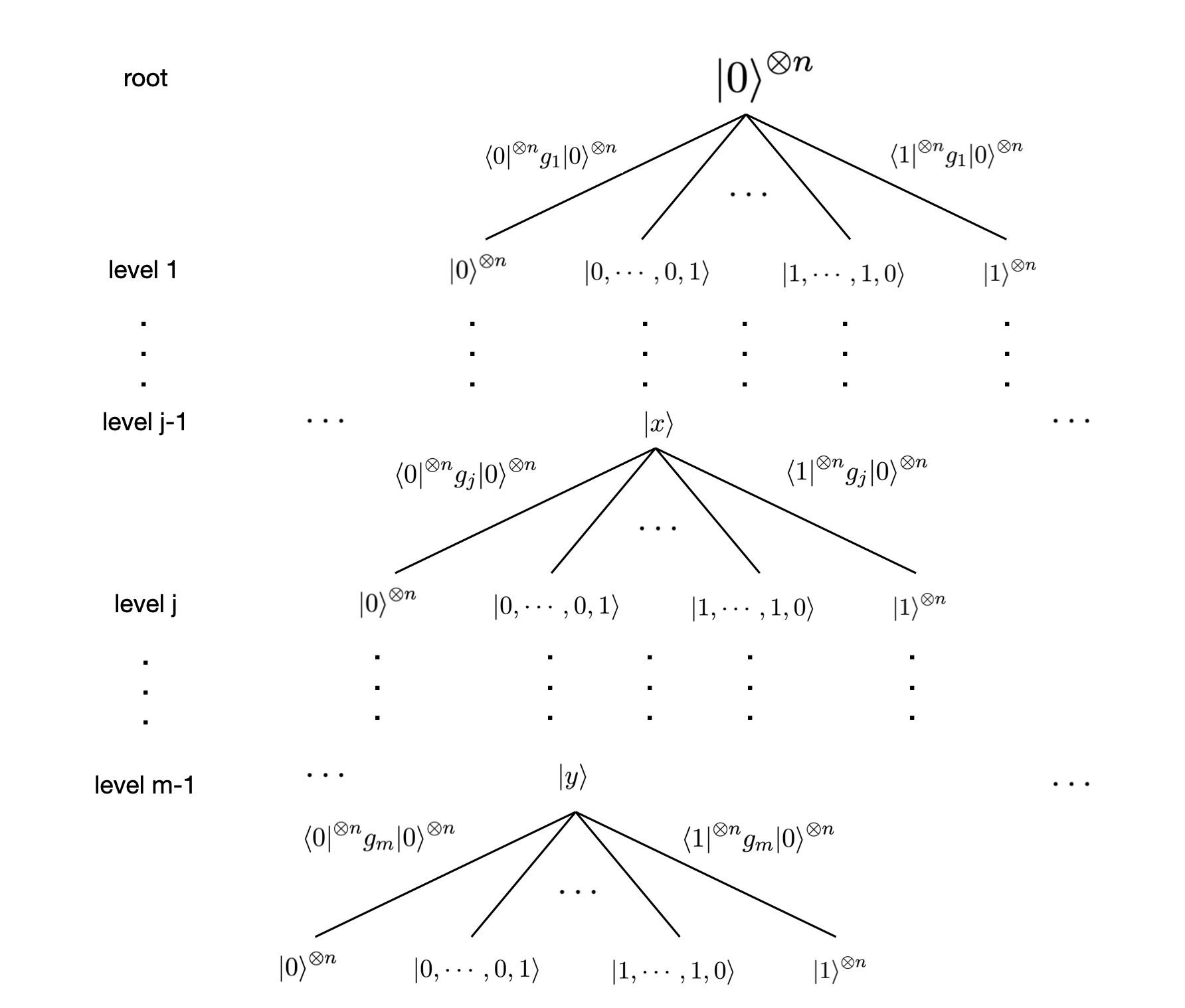
We will not dive into technical details here, this process can be seen as a form of dynamic programming, where the final probability is calculated by combining the probabilities of sub-paths in the tree. This process can be done in a polynomial amount of memory, which is the same as what is required for a P-SPACE **problem. Therefore, since **BQP problems can be solved efficiently using the sum of histories technique, which is a P-SPACE algorithm, it can be inferred that BQP is a subset of P-SPACE.
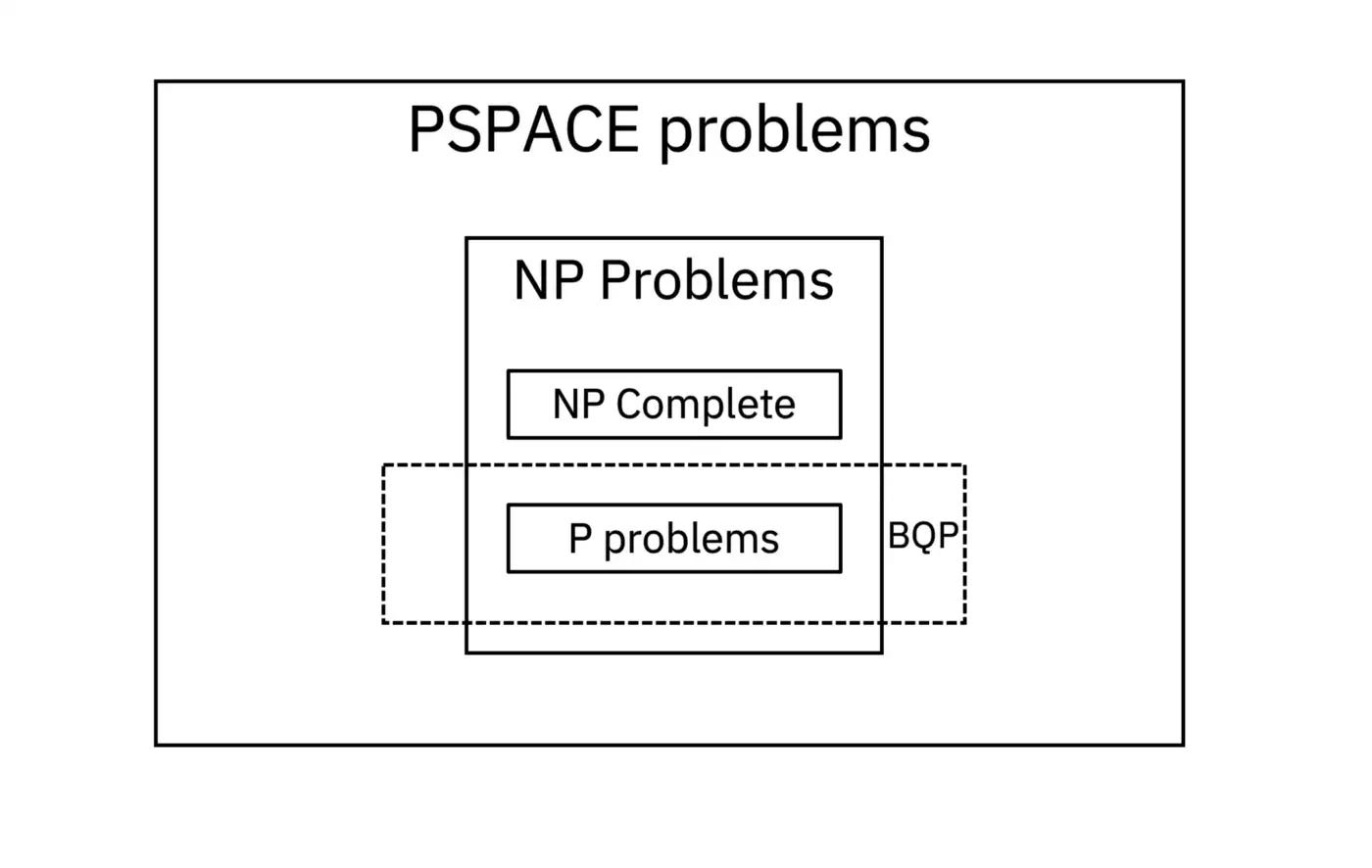
NP and BQP?
What is The Relation Between NP **and **BQP? As you might think, this question is an Unsolved problem in computer science, **unless the **P *vs** **NP* problem gets resolved, we won’t be able to give the exact relationship between these two classes. But, we saw that P⊆BQP, and it is conjectured that NP-complete problems like the *Traveling Salesman Problem *(TSP) **can’t be solved in polynomial time with bounded error even on quantum computers.
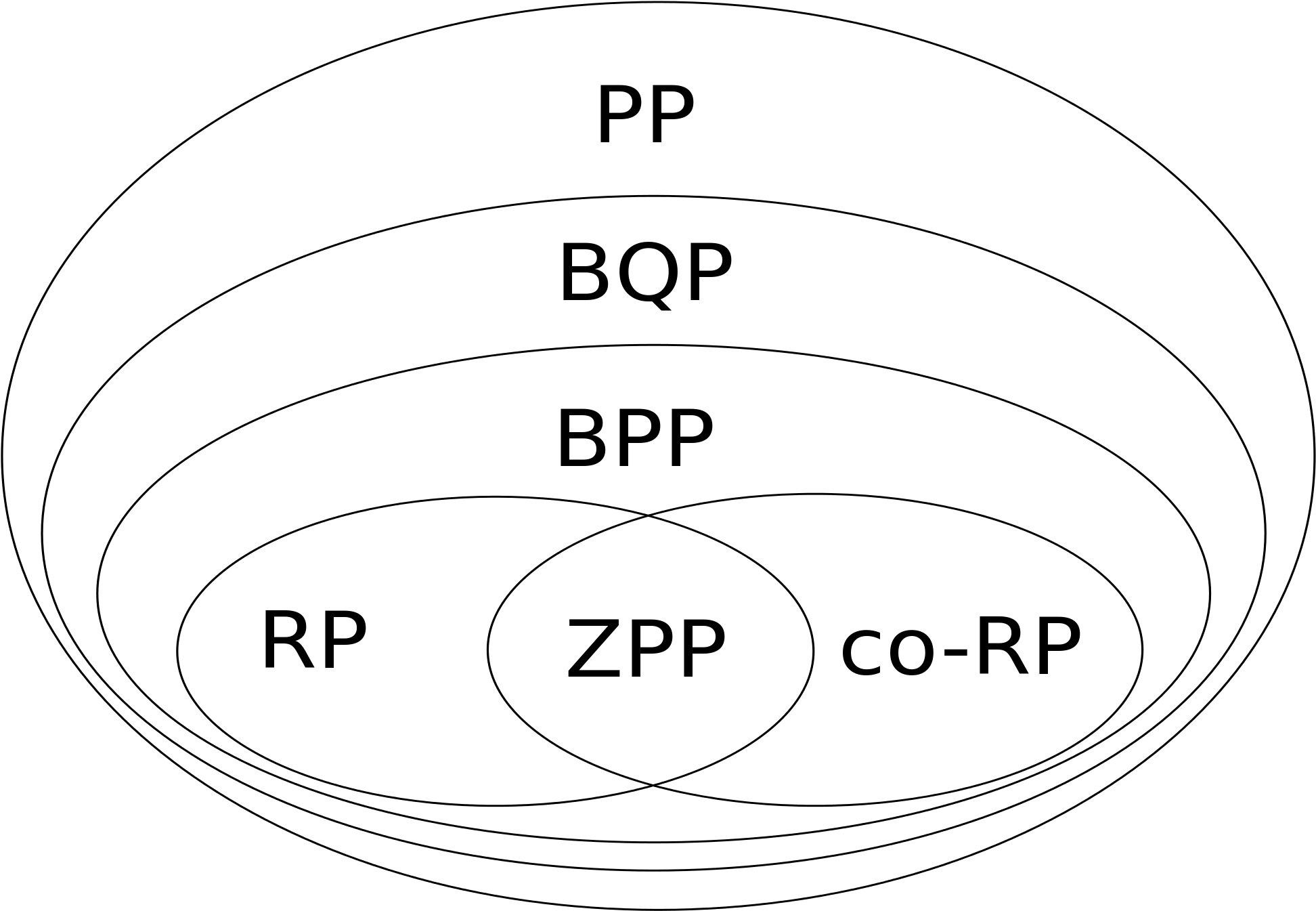
Better results are known for class **BQP **with respect to **BPP **and other probabilistic classes. Have a look at this diagram
If BQP = NP, it would imply that a quantum computer could efficiently solve all problems in NP, which would have significant implications for fields such as cryptography and optimization. However, if BQP **is not equal to **NP, it would mean that there are problems that a quantum computer can efficiently solve that a classical computer cannot, and it would provide a new class of problems for which quantum computers could be used.
The relationship between NP **and **BQP is a topic of ongoing research and debate in the field of theoretical computer science. While some researchers believe that a quantum computer could efficiently solve all problems in NP, others believe that there are fundamental differences between classical and quantum computation that will prevent this from being the case. It’s not been proven yet but it holds great potential to shape the field of quantum computing and could have significant implications for a wide range of industries and fields.

Reference
[1]Nielsen, Michael A.; Chuang, Isaac L. (2000), Quantum Computation and Quantum Information, Cambridge: Cambridge University Press, ISBN 0–521–63235–8, MR 1796805.
[2]E. Bernstein and U. Vazirani. Quantum complexity theory, SIAM Journal on Computing, 26(5):1411–1473, 1997. before-content : index.html