Quantum Computing Optimization Technique for Network Coding
Quantum Computers have the potential to outshine classical alternatives in solving specific problems, under the assumption of mature enough hardware. In this paper, I consider state-of-the-art of quantum computing. Additionally, a potential use case of quantum computing specific to communications and signal processing is presented.
Current quantum machines are limited in that they are noisy and only accommodate a small number of qubits, generally under 100. Additionally, gates are prone to error. For this reason, current approaches favor hybrid algorithms that combine classical and quantum methods to minimize required qubit and gate counts.
Working on a large amount of data requires a large quantum memory. However, there is no reliable quantum memory that would keep the quantum information for an arbitrarily long time and in large amounts. To get the most effective results, future quantum computing implementation will be in computing farms along with classical computers.
Clique Problem
In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. The maximum-clique-problem of an undirected graph is the largest subgraph in which an edge exists between every vertex.
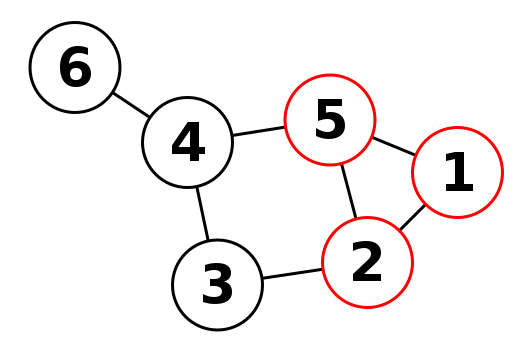
Clique Problems in Communications and Signal Processing
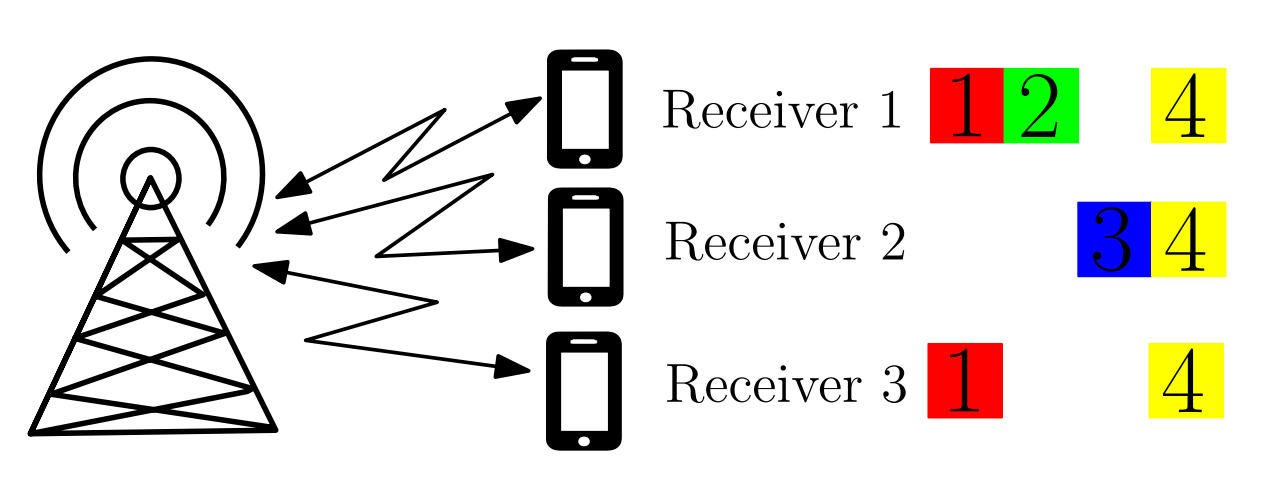
In their seminal paper[1], Ahlswede, Cai, and Yeung suggest mixing different information flows within intermediate nodes in the network, thereby increasing the information content per transmission. proved that Network Coding (NC) could enhance the transmission efficiency and throughput up to the network capacity.
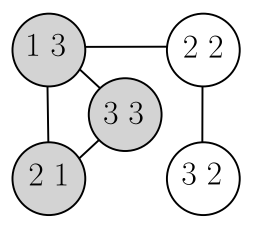
Consider a graph representing the coding possibilities for the system. Each clique in the graph represents a feasible packet combination. In particular, one can see that vertices 13, 21, and 33 represent a clique corresponding to transmitting the combination 1 ⊕ 3.
With such promising capabilities, network coding has been adopted by many researchers worldwide, to design high-data-rate communication algorithms. The schemes are further developed to meet the constraints of different communication scenarios, e.g., to improve security, quality of service, manageability, and robustness. Thanks to their combinatorial nature, problems in NC can often be formulated as graph theory problems in well-designed graphs.
Quantum Algorithm to Find Maximum Clique
In quantum computing, Grover’s algorithm, also known as the quantum search algorithm, refers to a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just O(√N**) **evaluations of the function, where *N *is the size of the function’s domain. It was devised by Lov Grover in 1996 [2]

The implementation of this algorithm involved iteratively checking whether the number of existing edges in each possible subgraph (clique) was larger than a reference k, growing from 1 to the total number of possible edges in the full graph. The superposition state of all vertex/edges represented in the qubits allowed making this comparison in one single quantum comparison for each k. The implementation successfully identified the maximum cliques of the graphs that were tested. The Algorithm work as follows:

Conclusion
An automated and generalized approach of quantum circuit synthesis for the max-clique *problem for any given undirected and unweighted graph has been proposed. Additionally, a potential use case of the *max-clique algorithm specific to solving problems in the field of communications and signal processing is presented.
[1] Hayssam Dahrouj, Ahmed Douek, A Tutorial on Clique Problems in Communications and Signal Processing (2020)
[2] L. K. Grover, “A fast quantum mechanical algorithm for database search,” Proceedings of the twenty-eighth annual ACM symposium on Theory of computing -STOC 96, 1996
[3] A. Haverly and S. Lopez. “Implementation of Grover’s Algorithm to solve the Maximum Clique Problem”. International Symposium on VLSI. July 2021
[4] U. Feige, G. Kortsarz, and D. Peleg, “The dense k-subgraph problem,” Algorithmica, vol. 29, p. 2001, 1999.
[5] Michal Kalina ,EPJ Quantum Technology volume, Quantum technology for military applications 2021
[6]A Comparison of Quantum Algorithms for the Maximum Clique Problem medium,Xanadu.
[7] Clique problem, Wikipedia
